Лекция
Тема: «Побитовые операции»
В Object Pascal над целыми типами (byte, shortint, word, integer, longint и и диапазоны) допустимы побитовые операции.
Логические операции над битами
Над битами 2-х целых операндов можно выполнять ранее рассмотренные логические операции: not, and, or, xor. Отличие между побитовыми и логическими операциями состоит в том, что побитовые (поразрядные) операции выполняются над отдельными битами операндов, а не над их значением в десятичном (обычном) представлении.
Например, число 5 в двоичном представлении (в одном байте) имеет значение 00000101. Операция not инвертирует биты, и мы получим 11111010, т.е. число 250. Если побитовую операцию
Введение
Побитовые операторы проводят операции непосредственно на битах числа, поэтому числа в примерах будут в двоичной системе счисления.
Я расскажу о следующих побитовых операторах:
- | (Побитовое ИЛИ (OR)),
- & (Побитовое И (AND)),
- ^ (Исключающее ИЛИ (XOR)),
- ~ (Побитовое отрицание (NOT)),
- << (Побитовый сдвиг влево),
- >> (Побитовый сдвиг вправо).
Битовые операции изучаются в дискретной математике, а также лежат в основе цифровой техники, так как на них основана логика работы логических вентилей — базовых элементов цифровых схем. В дискретной математике, как и в цифровой технике, для описания их работы используются таблицы истинности. Таблицы истинности, как мне кажется, значительно облегчают понимание битовых операций, поэтому я приведу их в этой статье. Их, тем не менее, почти не используют в объяснениях побитовых операторов высокоуровневых языков программирования.
О битовых операторах вам также необходимо знать:
- Некоторые побитовые операторы похожи на операторы, с которыми вы наверняка знакомы (&&, ||). Это потому, что они на самом деле в чем-то похожи. Тем не менее, путать их ни в коем случае нельзя.
- Большинство битовых операций являются операциями составного присваивания.
Побитовое ИЛИ (OR)
Побитовое ИЛИ действует эквивалентно логическому ИЛИ, но примененному к каждой паре битов двоичного числа. Двоичный разряд результата равен 0 только тогда, когда оба соответствующих бита в равны 0. Во всех других случаях двоичный результат равен 1. То есть, если у нас есть следующая таблица истинности:
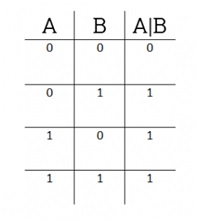
38 | 53 будет таким:
| A | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 |
| B | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 |
| A | B | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 |
В итоге мы получаем 1101112 , или 5510 .
Побитовое И (AND)
Побитовое И — это что-то вроде операции, противоположной побитовому ИЛИ. Двоичный разряд результата равен 1 только тогда, когда оба соответствующих бита операндов равны 1. Другими словами, можно сказать, двоичные разряды получившегося числа — это результат умножения соответствующих битов операнда: 1х1 = 1, 1х0 = 0. Побитовому И соответствует следующая таблица истинности:
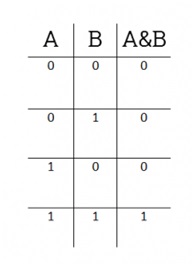
Пример работы побитового И на выражении 38 & 53:
| A | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 |
| B | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 |
| A & B | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 |
Как результат, получаем 1001002 , или 3610 .
С помощью побитового оператора И можно проверить, является ли число четным или нечетным. Для целых чисел, если младший бит равен 1, то число нечетное (основываясь на преобразовании двоичных чисел в десятичные). Зачем это нужно, если можно просто использовать %2? На моем компьютере, например, &1 выполняется на 66% быстрее. Довольно неплохое повышение производительности, скажу я вам.
Исключающее ИЛИ (XOR)
Разница между исключающим ИЛИ и побитовым ИЛИ в том, что для получения 1 только один бит в паре может быть 1:
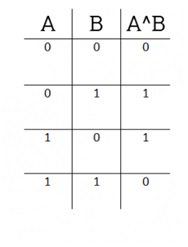
Например, выражение 138^43 будет равно…
| A | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 |
| B | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 |
| A ^ B | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
… 101000012 , или 16010
С помощью ^ можно поменять значения двух переменных (имеющих одинаковый тип данных) без использования временной переменной.
Также с помощью исключающего ИЛИ можно зашифровать текст. Для этого нужно лишь итерировать через все символы, и ^ их с символом-ключом.
Исключающее ИЛИ не самый надежный способ шифровки, но его можно сделать частью шифровального алгоритма.
Побитовое отрицание (NOT)
Побитовое отрицание инвертирует все биты операнда. То есть, то что было 1 станет 0, и наоборот.
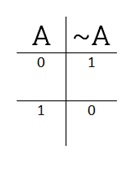
Вот, например, операция ~52:
| A | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| ~A | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 |
Результатом будет 20310
При использовании побитового отрицания знак результата всегда будет противоположен знаку исходного числа (при работе со знаковыми числами). Почему так происходит, узнаете прямо сейчас.
Дополнительный код
Здесь мне стоит рассказать вам немного о способе представления отрицательных целых чисел в ЭВМ, а именно о дополнительном коде (two’s complement). Не вдаваясь в подробности, он нужен для облегчения арифметики двоичных чисел.
Главное, что вам нужно знать о числах, записанных в дополнительном коде — это то, что старший разряд является знаковым. Если он равен 0, то число положительное и совпадает с представлением этого числа в прямом коде, а если 1 — то оно отрицательное. То есть, 10111101 — отрицательное число, а 01000011 — положительное.
Чтобы преобразовать отрицательное число в дополнительный код, нужно инвертировать все биты числа (то есть, по сути, использовать побитовое отрицание) и добавить к результату 1.
Например, если мы имеем 109:
| A | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 |
| ~A | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 |
| ~A+1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 |
Представленным выше методом мы получаем -109 в дополнительном коде.
Только что было представлено очень упрощенное объяснение дополнительного кода, и я настоятельно советую вам детальнее изучить эту тему.
Побитовый сдвиг влево
Побитовые сдвиги немного отличаются от рассмотренных ранее битовых операций. Побитовый сдвиг влево сдвигает биты своего операнда на N количество битов влево, начиная с младшего бита. Пустые места после сдвига заполняются нулями. Происходит это так:
| A | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| A<<2 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
Интересной особенностью сдвига влево на N позиций является то, что это эквивалентно умножению числа на 2N. Таким образом, 43<<4 == 43*Math.pow(2,4). Использование сдвига влево вместо Math.pow обеспечит неплохой прирост производительности.
Побитовый сдвиг вправо
Как вы могли догадаться, >> сдвигает биты операнда на обозначенное количество битов вправо.
Если операнд положительный, то пустые места заполняются нулями. Если же изначально мы работаем с отрицательным числом, то все пустые места слева заполняются единицами. Это делается для сохранения знака в соответствии с дополнительным кодом, объясненным ранее.
Так как побитовый сдвиг вправо — это операция, противоположная побитовому сдвигу влево, несложно догадаться, что сдвиг числа вправо на N количество позиций также делит это число на 2N. Опять же, это выполняется намного быстрее обычного деления.
