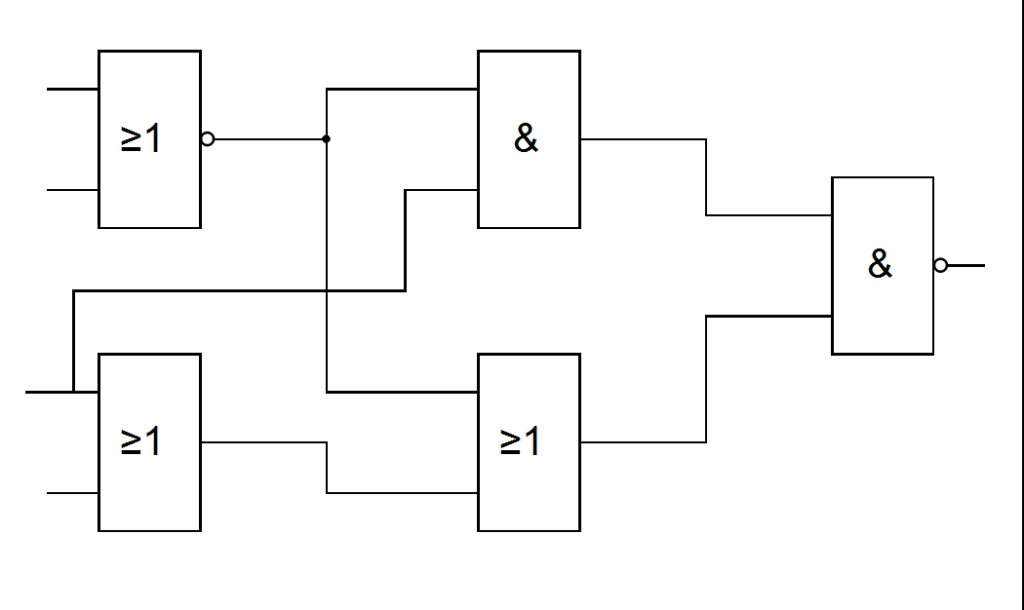
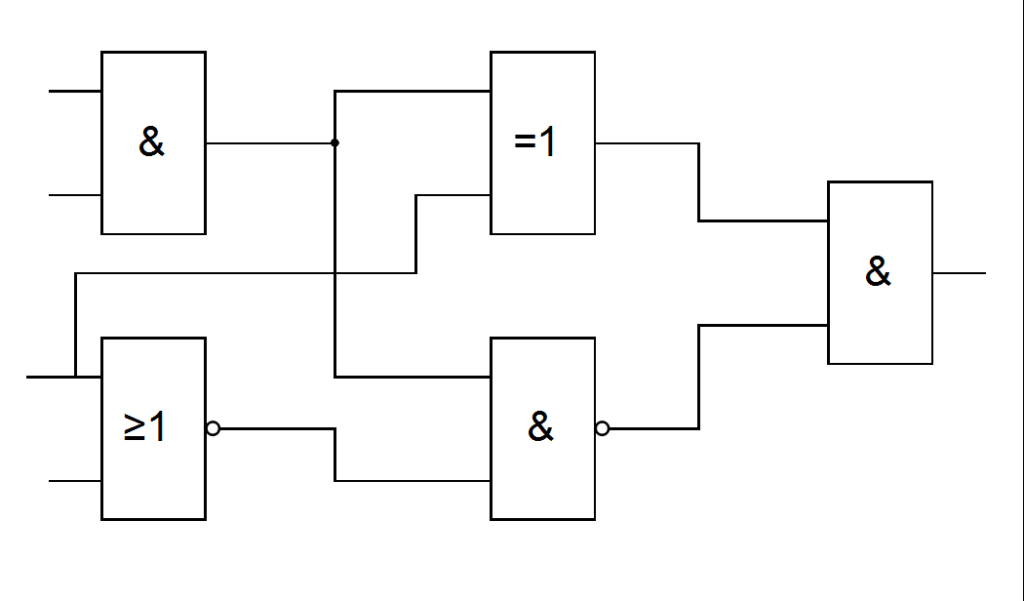
Практическая работа №2
Тема: «Исследование принципа работы логических элементов»
Цель: научиться составлять таблицы истинности для схем, представляющих собой различного рода комбинацию из простейших логических элементов
Теоретическое обоснование
Таблицы истинности
Логическая функция – это функция, у которой значения переменных и значение функции выражают логическую истинность.
Они могут принимать значения «истина» или «ложь» (1 или 0). Для функции, содержащей две переменные, наборов значений переменных всего четыре:
(1,1; 1,0; 0,1; 0,0)
Значения логических функций определяются с помощью таблицы истинности.
Таблицы истинности для основных двоичных логических функций
- Конъюнкция (логическое умножение) – сложное логическое выражение, которое является истинным только в том случае, когда истинны оба входящих в него простых выражения. Обозначение: A˄B
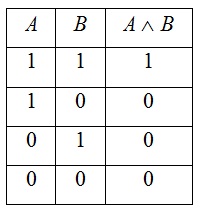
- Дизъюнкция (логическое сложение) – это сложное логическое выражение, которое истинно, если хотя бы одно из простых логических выражений истинно и ложно, если оба простых логических выражения ложны. Обозначение: A˅B
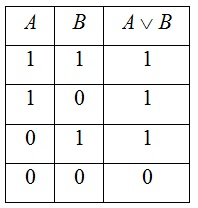
- Импликация (логическое следствие) – это сложное логическое выражение, которое является ложным тогда и только тогда, когда условие истинно, а следствие ложно.
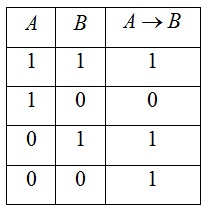
- Эквиваленция – это сложное логическое высказывание, которое является истинным только при одинаковых значениях истинности простых выражений, входящих в него.
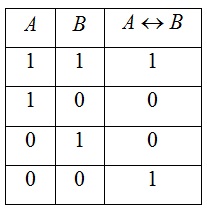
- Логическое отрицание (инверсия) делает истинное высказывание ложным и, наоборот, ложное – истинным.
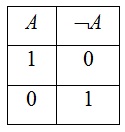
- Штрих Шеффера – операция, отрицающая конъюнкцию, т.е. значение ложно тогда и только тогда, когда оба простых выражения истинны.
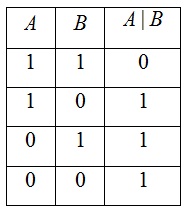
Как составить таблицу истинности?
Согласно определению, таблица истинности логической формулы выражает соответствие между всевозможными наборами значений переменных и значениями формулы.
Для формулы, которая содержит две переменные, таких наборов значений переменных всего четыре:
(0, 0), (0, 1), (1, 0), (1, 1).
Если формула содержит три переменные, то возможных наборов значений переменных восемь:
(0, 0, 0), (0, 0, 1), (0, 1, 0), (0, 1, 1), (1, 0, 0), (1, 0, 1), (1, 1, 0), (1, 1, 1).
Количество наборов для формулы с четырьмя переменными равно шестнадцати и т.д.
Удобной формой записи при нахождении значений формулы является таблица, содержащая кроме значений переменных и значений формулы также и значения промежуточных формул.
Примеры.
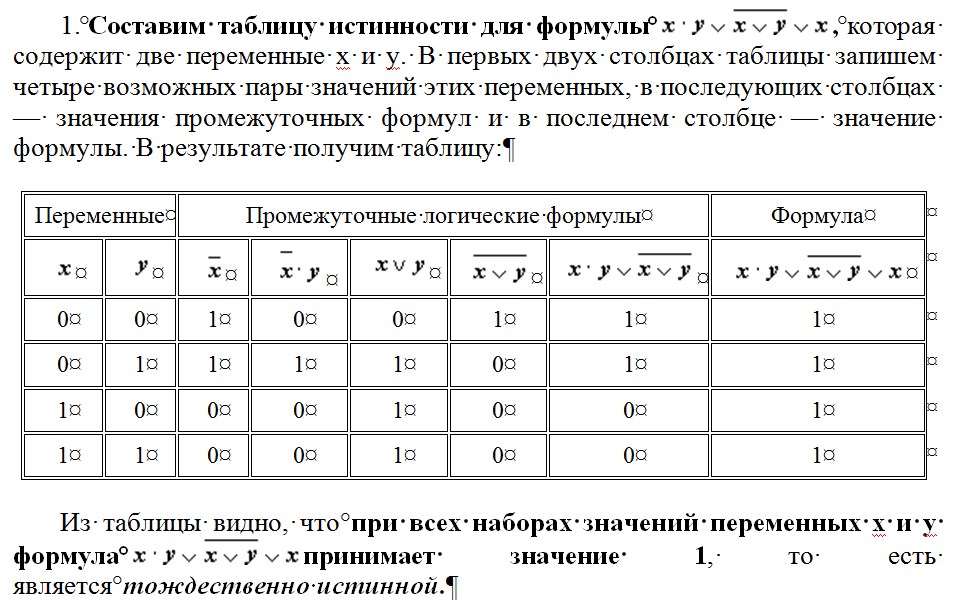
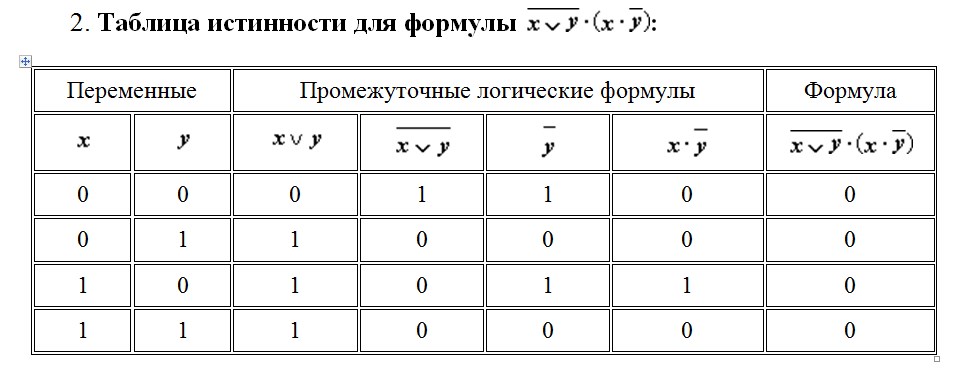
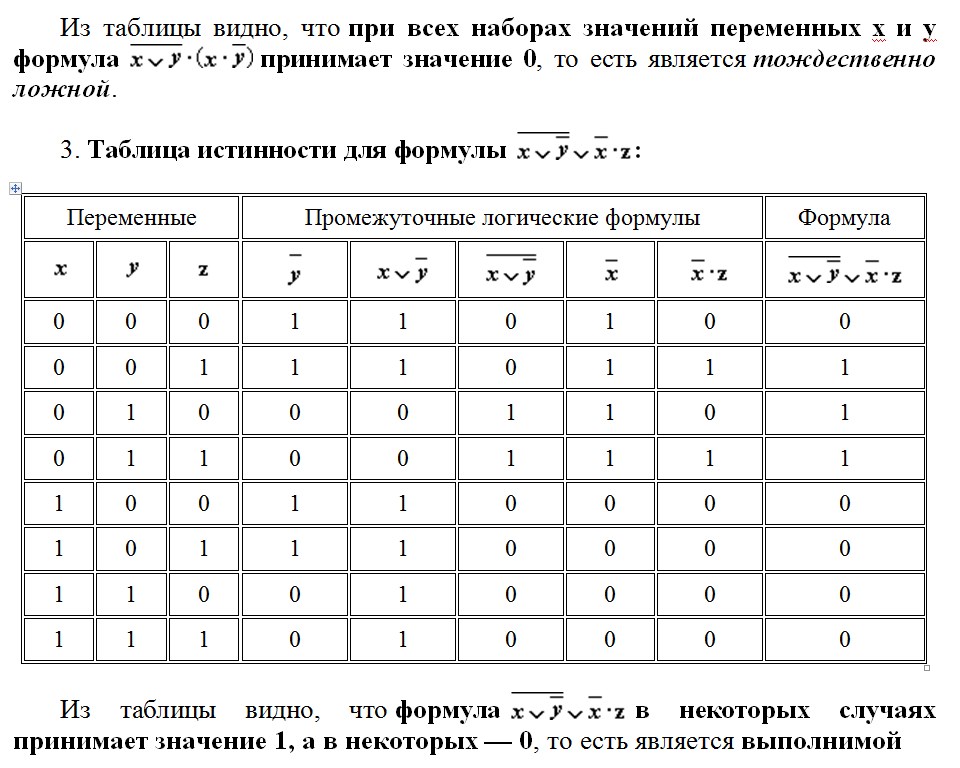
Пример таблицы истинности для наших схем
Обозначьте каждый элемент следующим образом:
Пронумеруйте каждый элемент и обозначьте DD1, DD2, … DDn, а также пронумеруйте входы в зависимости от количества входов X1, X2, … Xn. Например, вот так:
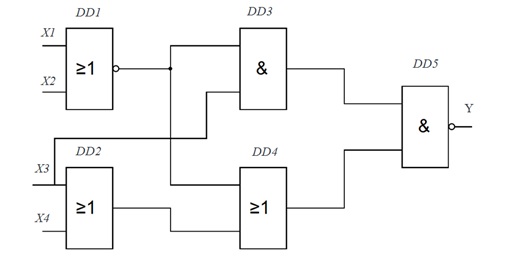
Далее смотрите на каждый элемент и анализируйте какой именно это элемент и находите соответствующую ему таблицу истинности, например: 1-й элемент – это «Исключающее ИЛИ»
Далее задайте входные сигналы, сначала следует взять все 0, например: 0,0,0,0. Первые 2 сигнала следует подавать на DD1, а следующие 2 – на DD2. Тогда на выходе первого элемента (и второго тоже) будет «0».
Элемент DD3
Cигнал c выхода элемента DD1 поступает на 1-й вход элемента DD3, а на 2-й вход поступает сигнал со входа X3 («0»), этот элемент называют «Логическим И», тогда при подаче 2-х входных сигналов «0» и «0» соответственно – на выходе будет «0» (поскольку 0*0=0).
Элемент DD4
На входы элемента DD4 («Исключающее ИЛИ») поступают сигналы DD1 и DD2 (это «0»), следовательно, на выходе будет «0».
Элемент DD5
Элемент DD4 – это «И-НЕ», т.е. происходит умножение 2-х сигналов, а затем инвертирование, т.е. на вход поступают два логических «ноля», далее они перемножаются 0*0, а затем происходит инвертирование, т.е. сигнал, обратный исходному, а это логическая «1». Следовательно, на выходе DD5 будет «1».
Затем составляется таблица истинности: по горизонтали число столбцов рассчитывается исходя из количества входных сигналов и элементов, а по вертикали – количество всевозможных входных комбинаций, которые определяются по формуле N=2i, где i – это количество входных сигналов. В нашем примере 4 входных сигнала и 5 элементов, тогда – 9 столбцов и 16 строк. Тогда таблица должна выглядеть следующим образом:

Ход работы
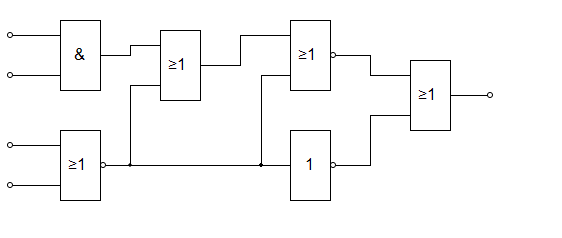
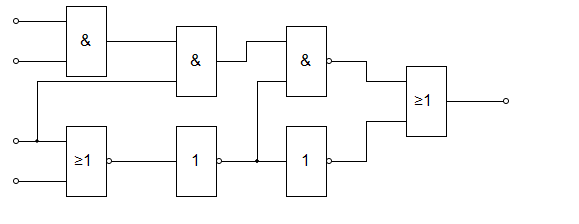
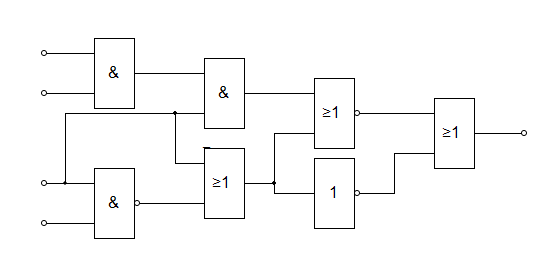
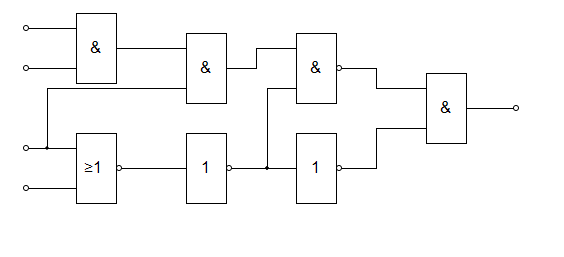
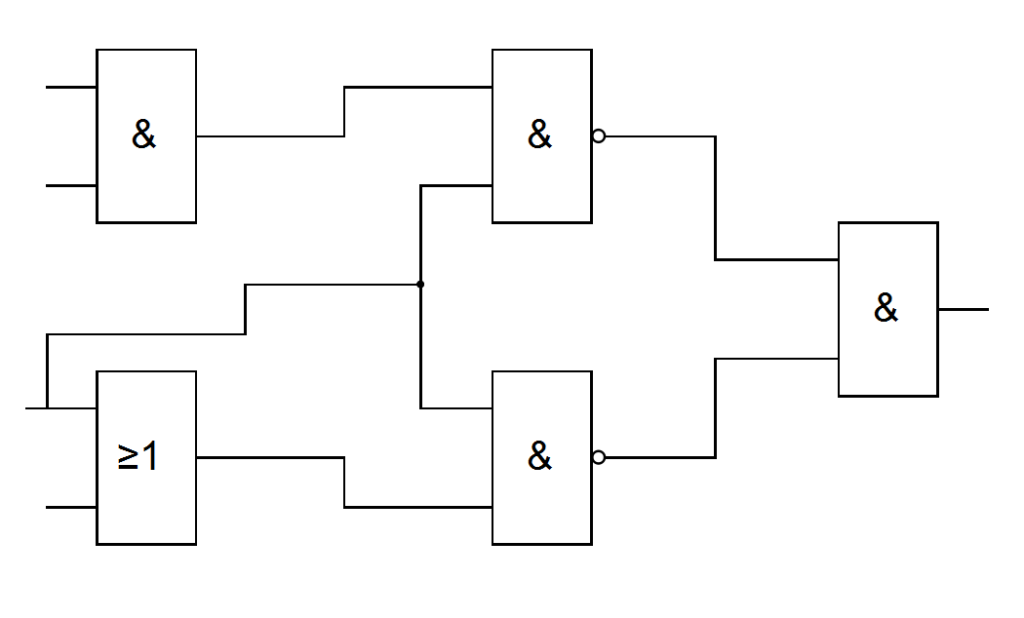
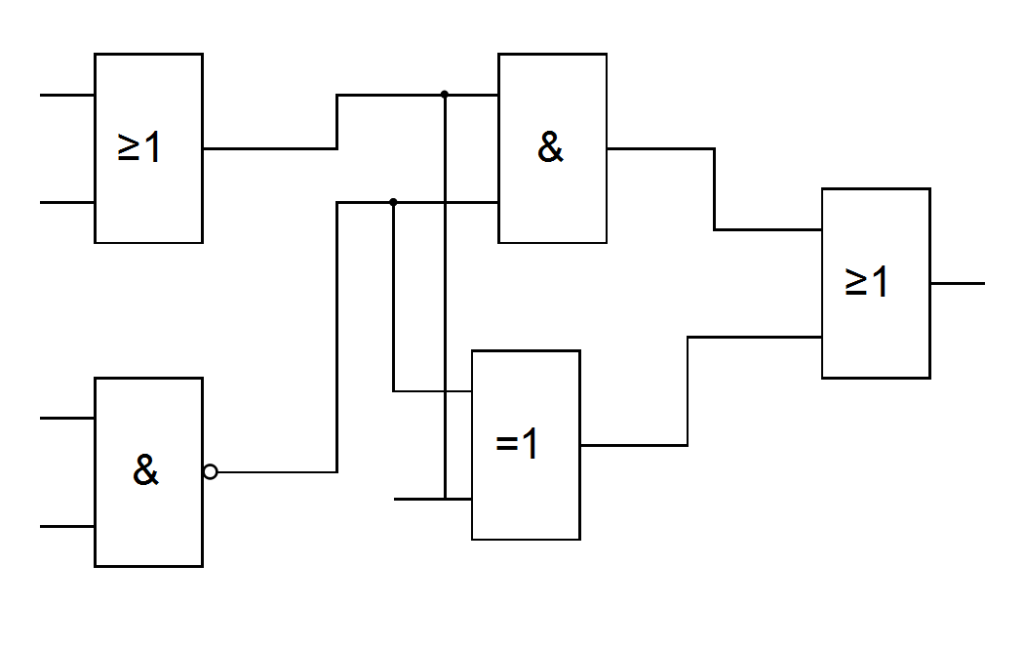
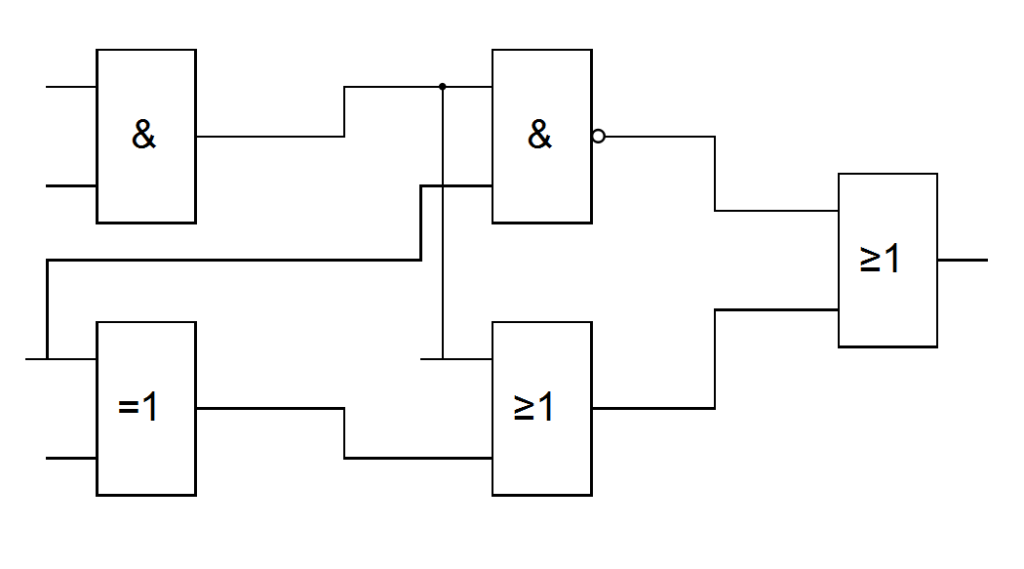
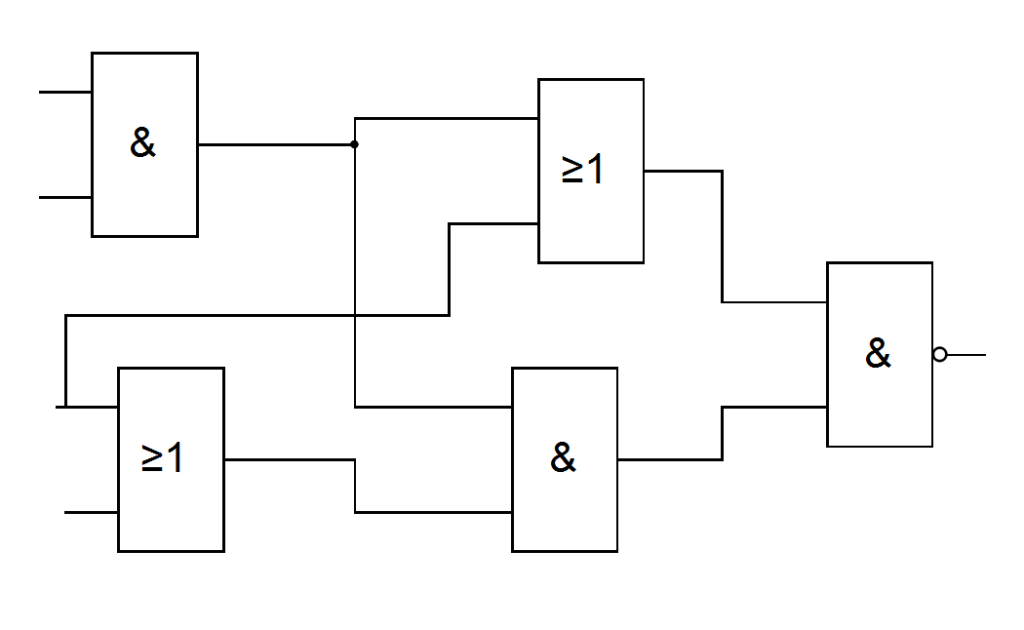
- Соберите схему в любом удобном приложении в соответствии с вариантом.
- Постройте таблицу истинности.
Варианты
Вариант 1, 11, 21